En la cadena de la tradición, que el tiempo engarza, hay un primer
eslabón y en él está el momento en el que aparece su verdad.
Emilio Lledó, El surco del tiempo.
Dartmouth College, 1955
En agosto de 1955, John McCarthy (Dartmouth College), Marvin L. Minsky (Harvard University), Claude E. Shannon (Bell Telephone Laboratories) y Nathaniel Rochester (I.B.M. Corporation) lanzaron A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence, documento que comenzaba con las siguientes palabras [40]:
Proponemos que 10 hombres durante 2 meses lleven a cabo un estudio sobre inteligencia artificial en el verano de 1956 en Dartmouth College en Hanover, New Hampshire. El estudio es para avanzar sobre las bases de la conjetura de que todo aspecto del aprendizaje o cualquier otra característica de la inteligencia puede en principio describirse tan precisamente que se puede hacer una máquina que la simule. Se intentará encontrar cómo hacer que las máquinas utilicen lenguaje, formen abstracciones y conceptos, resuelvan tipos de problemas ahora reservados a los humanos, y se mejoren a sí mismas. Pensamos que se puede hacer un avance significativo en uno o más de estos problemas si un grupo de científicos cuidadosamente seleccionados trabajan en ello juntos durante un verano.
Rochester era, junto con otro ingeniero, responsable del diseño del computador IBM Type 701 y había trabajado en el desarrollo del radar[41] y en máquinas de computación durante catorce años; también tenía experiencia en técnicas de programación automática, diseño de máquinas para hacer tareas hasta entonces solo reservadas a los humanos, o en simulación de redes nerviosas con particular énfasis en el uso de ordenadores para probar teorías neurofisiológicas. Shannon era ingeniero eléctrico y matemático, había desarrollado la teoría matemática de la información y la aplicación del cálculo proposicional (en su forma de álgebra de Boole) al análisis y la síntesis de los circuitos conmutados, estableciendo parte de las bases de la Teoría de la Información y la de la Electrónica Digital; sus intereses se extendían a la criptografía, las máquinas que aprenden y la teoría de máquinas de Turing. Minsky era profesor de Matemáticas y Neurología en Harvard, y había construido una máquina para simular el aprendizaje mediante redes neuronales. McCarthy era profesor de Matemáticas en Dartmouth College y había trabajado en una serie de cuestiones relacionadas con la naturaleza matemática del proceso de pensamiento, incluyendo la teoría de máquinas de Turing, la velocidad de computación, la relación de un modelo del cerebro con su entorno y el uso del lenguaje por las máquinas. Junto con Shannon había editado un número de Annals of Mathematics Study sobre La Teoría de Autómatas.
Con un presupuesto de 13.500 dólares (equivalentes a unos 150.000 en la actualidad) y una lista de invitados que incluía algunas de las mentes que han contribuido a conformar nuestra era[42], solicitaron a la Fundación Rockefeller soporte financiero para trabajar en diferentes aspectos del problema de la inteligencia artificial, unos formulados de manera colectiva y otros de manera individual por los proponentes. Podemos resumir los primeros como sigue:
- Si una máquina puede realizar un trabajo, entonces se puede programar un calculador automático (ordenador) para simularla. Las capacidades de velocidad y memoria de los actuales computadores pueden ser insuficientes para simular muchas de las funciones de alto nivel del cerebro humano, pero el principal obstáculo no es falta de capacidad de la máquina, sino nuestra falta de habilidad para escribir programas sacando el máximo provecho de lo que tenemos.
- ¿Cómo puede programarse un computador para utilizar un lenguaje? Se puede especular que una gran parte del pensamiento humano consiste en manipular palabras de acuerdo con reglas de razonamiento y reglas de conjetura. Así, formar una generalización consiste en admitir una nueva palabra y algunas reglas por las cuales las sentencias que la contengan implican y son implicadas por otras.
- ¿Cómo pueden ordenarse un conjunto de (hipotéticas) neuronas de manera que formen conceptos?
- Si tenemos un problema bien formulado, uno para el cual es posible examinar mecánicamente si una respuesta es válida o no, una manera de resolverlo es examinar todas las posibles respuestas de forma ordenada. Este método es ineficiente, y para excluirlo uno debe tener algún criterio para la eficiencia del cálculo, un método para medir la complejidad de los dispositivos necesarios, lo que implica tener una teoría de la complejidad de las funciones.
- Probablemente una máquina verdaderamente inteligente llevará a cabo actividades que pueden describirse como de automejora.
- Merece la pena clasificar qué tipos de ’abstracciones’ pueden definirse distintamente y cuáles no, y describir métodos para que una máquina forme abstracciones a partir de datos sensibles y de otro tipo.
- Una conjetura muy atractiva y por ahora claramente incompleta es que la diferencia entre pensamiento creativo y pensamiento competente no imaginativo estriba en la inyección de cierta aleatoriedad, pero ésta debe ser guiada por la intuición para ser eficiente. Es decir, la suposición formada o la corazonada incluyen aleatoriedad controlada en el razonamiento ordenado.
El proyecto se llevó a cabo en el verano de 1956 y, al utilizar por vez primera el término Inteligencia Artificial, se ha considerado el evento fundador de esta disciplina. Pero si Julieta pudo preguntarse:
¿Qué hay en un nombre? Eso que llamamos rosa
Tendría un olor tan fresco con cualquier otro nombre;(W. Shakespeare, Romeo y Julieta, Acto II, Escena II)
nosotros nos podemos preguntar si en dicho campo se estaba ya investigando, aunque refiriéndose a él con otros nombres.
El Ratio Club, 1949
En 1949 Londres tuvo el septiembre más caluroso que se había registrado hasta el momento, con temperaturas muy por encima de los 32 grados. De hecho, todo el verano había sido una mezcla de sol abrasador y salvajes tormentas. Así que fue una tarde inusualmente agradable el catorce de ese mes cuando una pandilla de científicos, [….], caminaba por la sucia capital bombardeada, una ciudad que se recuperaba lentamente de una guerra que había paralizado financieramente a Gran Bretaña. Convergieron en la frondosa Plaza de la Reina y se juntaron en una sala del sótano del hospital a las seis y media de la tarde. Después del jerez, la reunión comenzó a las siete.
Ésa fue la reunión inaugural del que pronto se conocería como Ratio Club, un grupo de neurólogos, biólogos, ingenieros, matemáticos y físicos relacionados con el ‘movimiento cibernético’ británico. Allí, en la planta baja del Hospital Nacional para Enfermedades Nerviosas, en el distrito de Bloomsbury, teniendo como techo la habitación de las enfermeras, se reunieron periódicamente desde 1949 hasta 1955; y allí, «después de un aperitivo y cerveza suficiente para lubricar las cuerdas vocales, los participantes escuchaban a un conferenciante o dos antes de enredarse en una discusión abierta»[43].
Aunque el libro de Norbert Wiener, Cibernética, o control y comunicación en el animal y la máquina[44], publicado en 1948, había disparado el interés por ese nuevo campo, como lo hicieron los artículos de Claude Shannon sobre teoría de la información[45], el requisito exigido a los miembros era haber tenido «las ideas de Wiener antes de aparecer su libro»[46]. Se trataba de reunir a gente que hubiera trabajado previamente en los mecanismos generadores del comportamiento y en el procesado de la información en el cerebro, el ‘control y comunicación’ a los que hacía referencia el título de Wiener, con ideas frescas. Muchos miembros estaban interesados en desarrollar dispositivos análogos al cerebro, bien como una manera de formalizar y explorar teorías sobre los cerebros biológicos, bien con el objetivo de crear máquinas inteligentes.
Kenneth Craik estuvo en la mente de los fundadores del Ratio Club, pero lamentablemente no pudo acompañarlos en la aventura: murió a los treinta y un años atropellado mientras iba en bicicleta por Cambridge el siete de mayo de 1945. Era psicólogo, le gustaban los dispositivos mecánicos y tenía gran talento para el diseño, y hoy es reconocido como pionero de los estudios de las interfaces hombre–máquina y padre del pensamiento cibernético. En 1943 había publicado The Nature of Explanation donde exponía una tesis radical: que el poder predictivo del pensamiento no es exclusivo de la mente humana, que no hay razón para que las propiedades esenciales de flexibilidad y versatilidad, reconocimiento y memoria, no pudieran ser emuladas por un dispositivo hecho por el hombre. Incluso llegó a decir que la mente humana es un tipo de máquina que construye modelos a pequeña escala de la realidad que después utiliza para anticipar acontecimientos[47]. Con una visión de largo alcance, anticipando tanto la cibernética como la inteligencia artificial y las ciencias cognitivas, veía el estudio de la mente como una investigación de los mecanismos capaces de generar comportamiento inteligente en máquinas biológicas y no biológicas[48].
Durante los años que el club estuvo activo[49] se trataron multitud de temas, aunque los dominantes fueron la teoría de la información, las técnicas y procesos probabilísticos y estadísticos, el reconocimiento de patrones, y los modelos del cerebro, analógicos y digitales, y todos ellos en el contexto de su aplicación para entender el sistema nervioso o desarrollar inteligencia en las máquinas. Además, había un tema implícito: el uso de artefactos en el marco del método sintético referido por Craik: el uso de modelos físicos para estudiar y probar hipótesis neurológicas o psicológicas. Los más famosos de esos artefactos fueron el homeostato de Ashby y las tortugas de Grey Walter.
§
William Ross Ashby (1903–1972), médico psiquiatra, había publicado en el número de marzo de 1949 de la revista Radio-Electronics el artículo “The Electronic Brain”, donde comparaba los tubos de vacío con las células nerviosas en cuanto a su funcionamiento, y decía que la invención de estos dispositivos electrónicos había transformado y enriquecido el significado de la palabra ‘máquina’ y hacía posible, cuando se ensamblan en un todo con sentido, la construcción de un cerebro. Y aclara [50] :
¿Y qué significa ‘tener sentido’ en un cerebro o en una máquina? Aquí podemos encontrar opiniones muy diferentes. Para algunos, la prueba crítica de si una máquina es o no un ‘cerebro’ sería si puede o no puede ‘pensar’. Pero para el biólogo el cerebro no es una máquina pensante, es una máquina actuante; recibe información y después hace algo con ella. Como cualquier otro órgano en el cuerpo animal, es un medio de supervivencia.
Es interesante atender a las tres ideas fundamentales presentes en este párrafo: (1) la distinción entre cerebro y mente, siendo el primero un órgano y la segunda lo que podríamos llamar una característica emergente; (2) la concepción de máquina como dispositivo que procesa información; (3) la concepción de máquina como medio para algo. La primera nos podría ayudar a entender lo que es inteligencia en general e inteligencia artificial en particular, o a distinguir inteligencia de capacidad de cálculo o de procesamiento. La segunda es un síntoma de aquel tiempo que anunciaba el nuestro, de un cambio de paradigma, del paso de la era mecánica a la era cibernética. La tercera nos retrotrae al origen etimológico de la palabra máquina.
La última propiedad mencionada, la de ser un medio de supervivencia, era para Ashby la clave para la construcción este ‘cerebro electrónico’, y él era uno de los que desde principios de los años 40 intentaban demostrar que la capacidad de adaptarse al entorno, de corregir desviaciones que alejen de un propósito central, y hacer esto de maneras diversas, en fin, la propiedad de ‘perseguir un objetivo’ (el ‘goal–seeking’ de Craik), no era privativa de la vida o de la mente, sino de la realimentación negativa, y cualquier máquina, animada o inanimada, que la tuviera exhibiría estas características. Pero ello no es suficiente para la supervivencia, sino que ésta supone la configuración de múltiples lazos de realimentación negativa y positiva —o en términos biológicos de tropismos negativos y positivos—, de mecanismos que permitan acercarse a lo beneficioso y alejarse de lo perjudicial, haciendo que la máquina «tenga que construir una parte esencial de su propio cableado». Ashby estaba aquí hablando no solo de adaptación, sino también de aprendizaje, o autoprogramación, asuntos que estaban entonces en pañales —y todavía no resueltos— pero cuyos principios empezaban a entenderse. Y también de ‘homeostasis’.
El concepto de homeostasis fue desarrollado originalmente por fisiólogo Walter Cannon quien lo utilizó para describir los mecanismos responsables de mantener dentro de unos márgenes ciertos parámetros en los organismos vivos, y la idea general sería muy influyente en el desarrollo de la cibernética. Ashby amplió los mecanismos homeostáticos descritos por Cannon[51] para incluir los de un sistema ‘ultraestable’, que él definía como un sistema con la capacidad de adaptar su propio entorno externo y su estructura interna para preservar su homeostasis general[52]. Un sistema de este tipo parece buscar una nueva forma viable, evitando la amenaza de un colapso mayor y potencialmente más catastrófico (un ser humano que siente frío y busca un ambiente más cálido es un ejemplo de esto). Un sistema ultraestable, argumenta Ashby, podría considerarse genuinamente inteligente, ya que desplegaría comportamientos complejos que le permitirían retener la integridad estructural[53]. Ashby desarrolló así una teoría general del comportamiento inteligente (es decir, la cognición) en torno a la idea central de la homeostasis biológica. Como demostrador construyó el homeostato (figura 2.1) con cuatro unidades de control de bombas de la Royal Air Force interconectadas. Con él ilustraba sus ideas adaptando automáticamente su configuración para estabilizar los efectos de cualquier perturbación introducida en el sistema.
§
Elmer y Elsie, las dos tortugas de W. Grey Walter, neurólogo estadounidense que se formó y trabajó en Reino Unido, fueron probablemente los primeros robots móviles, los primeros vehículos autónomos o los primeros robots inspirados en la biología, y en su tiempo fueron muy populares. Se movían con tres ruedas, disponían de un sensor óptico, otro háptico (de tacto), un motor para la propulsión, otro para el guiado y un ‘sistema nervioso’ basado en válvulas electrónicas, todo ello cubierto y protegido por un caparazón (ver figura 2.2). El propósito de Walter era mostrar que incluso en un sistema nervioso muy simple, de hecho cada tortuga tenía solo dos neuronas artificiales, puede surgir la complejidad por la interacción entre las distintas unidades, y su experimento «planteó una nueva cuestión de fisiología cerebral: si la complicación de las funciones cerebrales no derivaría tanto del número de unidades como de la abundancia de interconexiones»[54].
A pesar de la tecnología primitiva utilizada y de la sencillez del diseño, Walter pudo mostrar y observar comportamientos interesantes cuando los robots interactuaban con el entorno y entre ellos. La exploración del entorno era el modo de funcionamiento principal, de ahí el nombre de los artefactos o juguetes, como él los denominaba: Machina speculatrix. Eso los distinguía de otras máquinas que sólo buscaban un confort estático, como la machina sopora de Ashby (el homeostato), o la solución a un problema determinado, como la machina labyrinthea de Shannon, y la hacía una más plausible ‘imitación de la vida’:
No por su aspecto, sino por su actividad, el modelo debe parecerse al animal. Ha de tener, por tanto, los siguientes atributos, siquiera en parte: exploración, curiosidad, libre albedrío en el sentido de que su conducta sea impredecible, búsqueda de objetivos, autorregulación, evitación de dilemas, previsión, memoria, aprendizaje, olvido, asociación de ideas, reconocimiento de formas, y elementos de ajuste social. Tal es la vida [55].
Incluso creyó observar un extraño e inesperado comportamiento cuando uno de los robots pasó por delante de un espejo y ‘vio’ su propio reflejo: «… la maquinita se detiene ante los espejos y titila, oscila, trastabilla y baila como un torpe Narciso. Semejante conducta […] si fuera observada en un animal podría aceptarse como prueba de cierto grado de autorreconocimiento.» Y esto ocurría porque la máquina llevaba en la cabeza una luz que estaba encendida mientras exploraba y apagada cuando detectaba una luz exterior y se dirigía hacia ella; de forma que, ante un espejo, detectaba su propia luz que se apagaba en cuanto iniciaba la aproximación y, por tanto, la abortaba, produciendo así su particular trastabilleo y dándonos una muestra de una vía por la que lo simple puede engendrar lo complejo [56]. Vista la riqueza de comportamientos que podían exhibir Elsie y Elmer (Electro Light Sensitive with Internal and External stability — ELectro MEcanical Robot) con solo dos neuronas en lugar de los miles de millones de nuestros cerebros, Walter aventuró que no había «necesidad lógica o experimental de invocar algo más que el número para dar cuenta de nuestra convicción subjetiva de libre albedrío y nuestra conciencia objetiva de personalidad en nuestros semejantes.» [57].
§
Un asiduo visitante del Ratio Club era Warren McCulloch, neurofisiólogo estadounidense, participante en la reunión de Dartmouth, que en 1943 había publicado junto con el lógico Walter Pitts el artículo “A Logical Calculus of the Ideas Immanent in Nervous Activity” [58], donde, partiendo de la fisiología neuronal de Ramón y Cajal y de ciertas suposiciones físicas, proponían un modelo de neurona como unidad lógica ’todo o nada’ (booleana, 
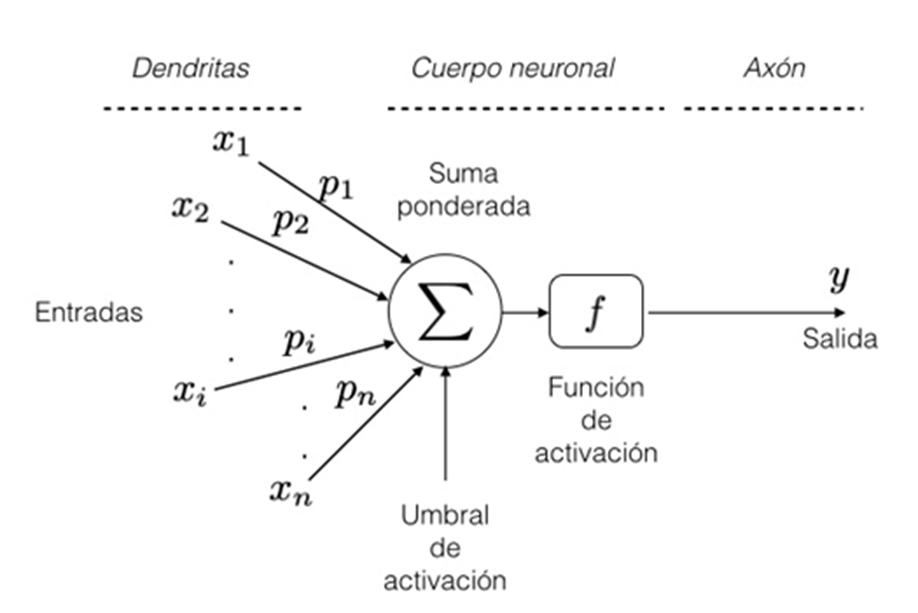
Figura 2.3. Modelo de McCulloch–Pitts de una neuronal artificial.
Turing y las máquinas
En las tortugas de Walter y en el homeostato de Ashby el comportamiento inteligente, la complejidad conductual, emergía del cuerpo, de la construcción de los artefactos. Alan Turing explorará un camino diferente, el de la inteligencia descorporeizada, computacional: sus contribuciones seminales, la máquina de Turing y el test de Turing, ni implican ni exigen realización física. De hecho, cuando Alan Turing conoció la intención de Ashby de construir el homeostato, le escribió sugiriéndole que podía realizar una simulación en su máquina universal (Automatic Computing Engine) en lugar de construir una máquina específica[62]. En su artículo sobre ‘números computables’[63] se describe originalmente la máquina que ostenta su nombre, cuyo funcionamiento Turing explica de la siguiente forma:
Podemos comparar a un hombre en el proceso de calcular un número real con una máquina que sólo es capaz de satisfacer un número finito de condiciones q1, q2, q3, … , qR que llamaremos
-configuraciones. La máquina se suministra con una cinta (el análogo del papel) que se mueve a lo largo de ella y se divide en secciones (llamadas ‘cuadrados’), cada una de las cuales puede llevar un ‘símbolo’. En cualquier momento hay un solo cuadrado en la máquina, digamos el r-ésimo, que lleva el símbolo G(r). Podemos llamar a este cuadrado el ‘cuadrado explorado’. Al símbolo en el cuadrado explorado le podemos llamar ‘símbolo explorado’. El ‘símbolo explorado’ es el único del que la máquina es, por así decirlo, ‘directamente consciente’. Sin embargo, al alterar su configuración la máquina puede recordar con eficacia algunos de los símbolos que ha ‘visto’ (explorado) previamente. El comportamiento posible de la máquina en cualquier momento está determinado por la m-configuración qn y el símbolo explorado G(r). Este par qn, G(r) se llamará la ‘configuración’: por tanto, la configuración determina el posible comportamiento de la máquina. En algunas de las configuraciones en las que el cuadrado explorado está en blanco (i.e. no tiene símbolo) la máquina escribe un nuevo símbolo en el cuadrado explorado; en otras configuraciones borra el símbolo explorado. La máquina también puede cambiar el cuadrado que se está explorando, pero solo desplazándolo un lugar hacia la derecha o hacia la izquierda. Además de cualquiera de estas operaciones la m-configuración puede cambiarse. Algunos de los símbolos escritos formarán la secuencia de cifras que constituye el decimal del número real que se está calculando. Los otros son solo notas toscas para ‘ayudar a la memoria’. Sólo estas notas toscas serán susceptibles de borrarse.
Afirmo que estas operaciones incluyen todas las que se utilizan en el cálculo de un número.
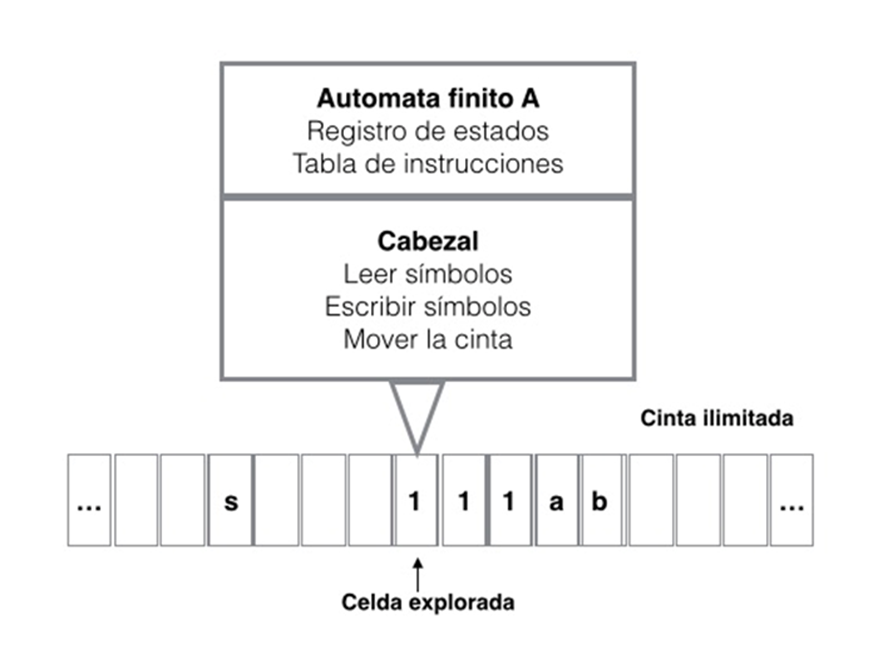
En la figura 2.4 podemos ver el esquema de una máquina de Turing. Consta de:
- Una cinta ilimitada dividida en celdas, cada una de ellas conteniendo un símbolo de algún alfabeto finito. El alfabeto contiene un símbolo especial llamado blanco (en la figura equivalente a ‘no símbolo’).
- Un cabezal (dispositivo D) que puede leer y escribir símbolos en la cinta y mover la cinta a la izquierda y a la derecha una (y sólo una) celda a la vez.
- Un registro de estados que almacena el estado de la máquina, uno de los estados finitos. (Parte del ‘autómata finito’ A.)
- Una tabla finita de instrucciones que, dado el estado actual y el símbolo que se está leyendo en la cinta, le dice a la máquina lo que hay que hacer: (1) borra o escribe un símbolo y entonces (2) mueve el cabezal y luego (3) asume el mismo o un nuevo estado como prescrito. (Parte del ‘autómata finito’ A.)
La simplicidad de la máquina viene desmentida por el propio Turing al afirmar que «estas operaciones incluyen todas las que se utilizan en el cálculo de un número». Teniendo en cuenta su analogía con el hombre que escribe sobre el papel y su concepción de la inteligencia como un proceso computacional (de cálculo) abstracto, su máquina inauguraba la teoría de autómatas, la era del autómata finito de propósito general (el ordenador, del que estaría definiendo también la ‘arquitectura’ conocida popularmente como de von Neumann: una unidad de procesamiento que contiene una unidad aritmético lógica y registros del procesador, una unidad de control que contiene un registro de instrucciones y un contador de programa, una memoria para almacenar tanto datos como instrucciones, almacenamiento masivo externo, y mecanismos de entrada y salida) y de la inteligencia artificial.
Daría un paso más en 1950 en su artículo “Maquinaria computacional e inteligencia”[64]. El artículo empieza con estas palabras, que son toda una declaración de principios:
Propongo considerar la cuestión, ‘¿Pueden pensar las máquinas?’ Esto debería empezar con definiciones del significado de los términos ‘máquina’ y ‘pensar’.
Para sustituir (eludir) la cuestión, propone un juego, ‘el juego de la imitación’, un test sencillo para determinar si una máquina puede pasar por un humano en una conversación escrita, un juego que, según Turing, «está estrechamente relacionado con ella y se expresa en palabras relativamente no ambiguas»; y la concepción de esta relación estrecha expone sin ambigüedad la idea que Turing tenía sobre el pensamiento, su reduccionismo[65]. En el juego participan un interrogador humano que tiene que distinguir entre dos sujetos, uno humano y otro artificial, con los cuales solo se puede comunicar, como hemos dicho, mediante mensajes escritos. Los detalles sobre la realización física de la máquina no se consideran relevantes para la cuestión de si es o no inteligente, en claro contraste con Ashby y Walter, y no es preciso que interactúe directamente con el interrogador y, por lo tanto, no hay necesidad de programarla para reconocer o ejecutar aspectos tales como el lenguaje corporal o la entonación, fundamentales en la comunicación cara a cara. Tras describir el juego y defender que le sirve como equivalente inequívoco de la pregunta original, Turing aclara que el objetivo del mismo para la máquina es ‘pasar por’ un ser humano dentro de los límites establecidos, y por ello lógicamente supone que la mejor estrategia de la máquina consiste en «intentar proporcionar las respuestas que el hombre daría con naturalidad»[66]. El resto del ensayo, pues así deberíamos llamarlo y no artículo, está dedicado a definir los términos ‘máquina’ y ‘pensar’ que está considerando. En seguida aclara que las máquinas que participan en él son las ‘computadoras digitales’. Su estructura, con su ‘almacén’ o memoria donde se guardan los datos y ‘la tabla de instrucciones’ o programa, su ‘unidad ejecutiva’ encargada de realizar las operaciones, y su unidad de ‘control’ que vela por que estas instrucciones se lleven a cabo correctamente (procedimiento y orden), hace que estas máquinas puedan «imitar cualquier máquina de estados discretos» y, por lo tanto, las hace «máquinas universales»: pueden llevar a cabo cualquier tarea de cómputo «adecuadamente programada»[67]. De manera igualmente expedita (y elusiva) aclara su opinión sobre el segundo de los términos diciendo que la «cuestión original, ‘¿Pueden pensar las máquinas?’, … tiene demasiado poco sentido para merecer una discusión», que tal vez «a finales de siglo el uso de las palabras y la opinión general educada se habrán alterado tanto que uno será capaz de hablar de máquinas que piensan sin esperar ser contradicho»[68]; y procede seguidamente a considerar y refutar opiniones contrarias a la suya: que el pensamiento es una función del alma inmortal del hombre, que las consecuencias de que las máquinas pensaran serían demasiado tristes y es mejor no considerarlo, que la lógica matemática puede utilizarse para demostrar que la capacidad de las máquinas de estado está limitada, que las máquinas no pueden ser conscientes, que no pueden hacer todo lo que hace el ser humano, que las máquinas son incapaces de crear o innovar, que el sistema nervioso no es una máquina de estados discretos y por lo tanto no es posible imitar con ellas su comportamiento, que el comportamiento humano no se puede formalizar en un conjunto de reglas, e incluso que las máquinas son incapaces para la percepción extrasensorial de la que parecen estar dotados algunos humanos. En fin, casi abarca por completo el espectro de objeciones e inquietudes que, por lo que vemos, ha llegado casi intacto a nuestros días. Solo se detiene a considerar con detalle la que él llama ‘la objeción de Lady Lovelace’.
§
En el año 1770, en la corte de la emperatriz austriaca María Teresa, un inventor llamado Wolfgang von Kempelen presentó una máquina que jugaba al ajedrez. El Turco, como Kempelen llamó a su invento, era un autómata de tamaño natural tallado en madera de arce y vestido con túnicas otomanas, que estaba sentado detrás de un mueble de madera con un tablero de ajedrez encima. Kempelen afirmaba que la máquina podía derrotar a cualquier miembro de la corte, y uno de los asesores de María Teresa aceptó el desafío. Kempelen abrió las puertas de la cabina para mostrar un mecanismo similar a un reloj, una intrincada red de palancas y engranajes, y luego insertó una llave en la máquina y le dio cuerda. El autómata cobró vida, levantando su brazo de madera para mover la primera pieza de ajedrez. En treinta minutos había derrotado a su adversario. Durante la siguiente década Kempelen recorrió con su máquina toda Europa, derrotando, según cuenta la leyenda, a algunos de las más formidables mentes de la época, incluidos Benjamín Franklin, Napoleón y Federico el Grande. A la muerte de von Kempelen en 1804, el Turco fue comprado por Johann Nepomuk Maelzel, un estudiante universitario alemán y constructor de instrumentos, que continuó la gira mundial[69]. Charles Babbage, famoso ingeniero y matemático británico[70], jugó contra el Turco dos veces en 1819, y perdió ambas partidas. Babbage sospechaba que el autómata no era ‘inteligente’, sino simplemente un elaborado engaño, que ocultaba a una persona que, de alguna manera, estaba controlando los movimientos del Turco desde el interior. Y tenía razón: un maestro del ajedrez movía los brazos del Turco mediante una especie de pantógrafo; un humano era ‘el alma de la máquina’, tal como había supuesto en 1835 Edgar Alan Poe en su ensayo El jugador de ajedrez de Maelzel, donde expone una solución del misterio[71]. El Turco, el truco podríamos decir, no era sino una secularización o profanación de las ‘máquinas de Dios’[72] estudiadas por Descartes, o de la cabeza parlante de Roger Bacon citada en el capítulo anterior, pero estimuló a Babbage que a partir de 1830 empezó a trabajar en una Máquina Analítica con un ‘almacén’ y un ‘taller’ (a modo de memoria y procesador) y la capacidad de interpretar instrucciones codificadas en tarjetas perforadas. Imaginó esta máquina tan sólo como una mejora de su proyecto anterior, la Máquina Diferencial concebida para hacer tablas de logaritmos, pero su ayudante, Ada Lovelace, se dio cuenta de que la programabilidad daba a la máquina una funcionalidad general, y concibió un nuevo tipo de ‘ciencia poética’ con la cual los matemáticos podrían enseñar a la máquina incluso a componer «elaboradas y científicas piezas de música»[73]. Esa nueva ciencia poética sería la programación, el software.
Augusta Ada King, condesa de Lovelace (Londres,1815–1852), hija de Lord Byron y conocida habitualmente como Ada Lovelace, fue una matemática y escritora, célebre sobre todo por su trabajo en la Máquina Analítica. Entre sus notas sobre la máquina se encuentra lo que se reconoce hoy como el primer algoritmo destinado a ser procesado por una máquina, por lo que se la considera como la primera programadora de ordenadores y hoy da nombre a un lenguaje de programación de alto nivel. La objeción que Turing llama ‘de Lady Lovelace’ viene formulada en palabras sacadas de un escrito que ella misma redactó sobre la Máquina Analítica de Babbage y que Turing cita:
La Máquina Analítica no tiene pretensiones de originar nada. Puede hacer cualquier cosa que nosotros sepamos ordenarle hacer [74].
Es decir, aunque concibió un nuevo tipo de ‘ciencia poética’ con la cual los matemáticos podrían enseñar a la máquina incluso a componer «elaboradas y científicas piezas de música»[75], Lady Lovelace, según Turing, no concebía ninguna originalidad en su funcionamiento, sólo método, y por tanto no podría hacer nada nuevo. Pero, dice Turing, «¿Quién puede estar seguro de que el ‘trabajo original’ que ha hecho no es simplemente el crecimiento de la semilla plantada en él por la enseñanza, o el efecto de seguir principios generales bien conocidos?»[76]. Esta es la base sobre la que establece su conclusión defendiendo la posibilidad de que las máquinas aprendan y de que de lo aprendido surja algo nuevo y no previsto, algo original. Lanzaba esta idea con el símil de un reactor nuclear: una idea inyectada en la máquina corresponde a un neutrón que entra en el reactor; si el tamaño de éste es menor que el crítico el neutrón causará una perturbación que se extinguirá; pero si el tamaño del reactor es lo suficientemente grande la perturbación causada por el neutrón crecerá hasta destruirlo. Turing se pregunta [77]:
¿Existe un fenómeno correspondiente para las mentes y hay uno para las máquinas? Parece haber uno para la mente humana. La mayoría de ellas parecen ser ‘subcríticas’, es decir, corresponden en esta analogía a reactores de tamaño subcrítico. Una idea presentada a una mente así dará lugar en promedio a menos de una idea en respuesta. Una pequeña proporción es ‘supercrítica’. Una idea presentada a una mente así puede dar lugar a una ‘teoría’ completa que consta de ideas secundarias, terciarias y aún más remotas. Las mentes de los animales parecen ser definitivamente subcríticas. Siguiendo esta analogía preguntamos: ¿Se puede hacer que una máquina sea supercrítica? [78]
Turing no responde directamente a esta pregunta, pero afirma que las máquinas tendrán suficiente capacidad de almacenamiento para ser comparables al cerebro humano, y que el único problema es «averiguar cómo programarlas para que estas máquinas puedan participar en el juego»[79]. La solución que propone es conseguir que las máquinas aprendan y divide el problema en dos partes: programar la mente de un niño y llevar a cabo después el proceso de educación. Haciendo un paralelo con la evolución, identifica el material hereditario con la estructura de la máquina–niño, y los cambios en la estructura con las mutaciones, que aquí irían guiadas por la inteligencia de quien lleva a cabo el experimento y no enteramente por el azar; el experimentador haría también de selección natural, lo que permitiría acelerar enormemente el proceso.
Alan Turing, desde luego, tenía una mente supercrítica (acorde con el tamaño de su cabeza, según parece), y en solo dos trabajos nos puso tareas para un siglo. Lamentablemente él murió en 1954 y no pudo ayudarnos mucho más [80].
La tercera fuente
Antes de morir, cuando lo detuvieron por su condición homosexual, en una carta a un amigo escribió este silogismo [81]:
Turing cree que las máquinas piensan
Turing yace con hombres
Luego las máquinas no piensan
Hasta el momento hemos visitado brevemente las dos fuentes principales de las que surgiría la inteligencia en las máquinas: la imitación de la vida o la consideración del cerebro como una máquina de actuar, y la consideración del cerebro como una máquina de calcular. Ahora nos toca aludir a la tercera fuente: la filosofía, y en particular la lógica, o la consideración del cerebro como una máquina de razonar [82].
El silogismo antes citado lleva otro implícito:
Turing cree que las máquinas piensan
Turing yace con hombres
Los hombres que yacen con hombres tienen la mente perturbada
Luego Turing tiene la mente perturbada
Luego las máquinas no piensan
y sería difícil encajarlo en alguno de los modos y figuras estudiados por Aristóteles. Es un falso silogismo que no cumple con la definición: «silogismo es aquel discurso en el que, sentadas ciertas proposiciones [premisas], de ellas se sigue necesariamente algo distinto de lo previamente establecido [conclusión]»[83]. Su falsedad estriba en la mayor (G) del silogismo implícito:
Si el hombre que yace con hombres tiene la mente perturbada (Si todo M es G) y Turing yace con hombres (y todo P es M), entonces Turing tiene la mente perturbada (entonces todo P es G): silogismo modo Barbara.
La filosofía griega, sobre todo a partir del Organon de Aristóteles, dejó establecidas ciertas ‘leyes del pensamiento’ que se ocupan de los principios de la inferencia válida, es decir, de argumentar válidamente y de los principios de validez, y desde entonces la lógica es una herramienta fundamental para toda indagación o discurso que demanda una demostración, pues demostrar una proposición no es sino inferirla válidamente de premisas verdaderas[84]. Todas las deducciones y demostraciones empleadas por la ciencia tienen aquí su origen, y aunque esta lógica pareció obsoleta gracias a los desarrollos de la lógica matemática en los siglos XIX y XX, ha cobrado de nuevo importancia en campos tales como la teoría de la argumentación que se utiliza en inteligencia artificial[85], y que tanto ayudaría en el juego de la imitación propuesto por Turing. Esta lógica clásica, de la que Aristóteles se considera el fundador, dejó establecidos tres axiomas o principios fundamentales: el principio de no contradicción, el principio de identidad y el del tercio excluso o tercero excluido. Éste último ha tenido a lo largo de la historia muchas versiones desde Aristóteles en su Metafísica[86]: «Llamo demostrativas las opiniones comunes a partir de las cuales se efectúa toda demostración, como por ejemplo ‘toda cosa tiene que ser afirmada o negada’ y ‘es imposible que una cosa sea y no sea simultáneamente’». Nosotros lo podemos formular como que la proposición A o no A (A ∨ ¬A) es siempre verdadera. Mas en su obra Sobre la interpretación Aristóteles dice que «en las cosas que son y que fueron, es necesario que o la afirmación o la negación sea verdadera o falsa; y [de las contradictorias] sobre los universales como universales siempre la una [ha de ser] verdadera y la otra falsa, y también sobre los singulares…. En cambio, con los singulares futuros no [ocurre] igual», y a continuación analiza algunos de los absurdos lógicos a los que se llega al aplicar la ley del ‘tercio excluso’ a las cosas por venir. Pasando del dicho al hecho, las «cosas reales … o serán o no serán no por afirmarlas o negarlas», sino que «el origen de lo que ha de ser radica en el deliberar y en el hacer algo [previo], y que, en general, en las cosas que no siempre se realizan existen la posibilidad de que sean y de que no sean»[87]. Aunque el asunto dio mucho que hablar a lo largo de la Edad Media y la Edad Moderna, y aunque, como hemos visto, ya Aristóteles nos había dado un atisbo de una región intermedia para esta lógica bivalente en la que lo verdadero y lo falso podrían confundirse o al menos convivir, hubo que esperar a que en los años veinte del pasado siglo Jan Łukasiewicz propusiera una lógica trivalente en la que entre lo verdadero y lo falso estaba lo ‘posible’. Argumentaba esta posibilidad utilizando los ‘singulares futuros’ o ‘futuros contingentes’ del estagirita[88]:
Puedo suponer sin contradicción que mi presencia en Varsovia en un cierto momento del año próximo –-por ejemplo, al mediodía del 21 de diciembre— no está en el presente instante determinada ni positiva ni negativamente. Por tanto, es posible, pero no necesario, que yo esté presente en Varsovia en ese momento dado. En este supuesto, la proposición «estaré en Varsovia a mediodía del 21 de diciembre del año próximo» no puede, en el presente instante, ser ni verdadera ni falsa. Porque si fuera verdadera ahora mi futura presencia en Varsovia tendría que ser necesaria, lo cual está en contradicción con el supuesto. Si, por otra parte, fuera falsa ahora, mi presencia futura en Varsovia tendría que ser imposible, lo cual también contradice el supuesto. Por lo tanto, la proposición en cuestión no es, en este momento, ni verdadera ni falsa y debe poseer un tercer valor, distinto de «0» o falsedad y de «1» o verdad. Este valor se puede designar por «1/2». Representa «lo posible», y se añade como tercer valor junto a «lo verdadero» y «lo falso».
Propuso lógicas multivaluadas cuya base era distribuir los valores de verdad de manera uniforme sobre el segmento real [0,1]: si se trata de 
Claramente, la ‘clase de todos los números reales que son mucho mayores que
’, o ‘la clase de mujeres hermosas’, o ‘la clase de hombres altos’, no constituyen clases o conjuntos en el sentido matemático habitual de estos términos. Sin embargo, el hecho es que estas ‘clases’ definidas de manera imprecisa juegan un papel importante en el pensamiento humano, particularmente en los dominios del reconocimiento de patrones, la comunicación de la información y la abstracción.
La lógica borrosa de Zadeh se puede ver como una extensión de la lógica polivalente, análoga a la extensión de los números racionales para formar el conjunto de los reales, y tal vez el hecho de ser propuesta por un ingeniero eléctrico, que la sacó del abstracto y exclusivo mundo de la lógica matemática, en un momento de efervescencia intelectual, fue determinante e hizo que pasara de forma casi inmediata a integrar el corpus de las herramientas de la inteligencia artificial con aplicaciones prácticas.
[40] McCarthy, J., Minsky, M. L., Rochester, N., and Shannon, C. (1956). A proposal for the Dartmouth Summer Research Project on Artificial Intelligence. http://www-formal.stanford.edu/jmc/history/dartmouth/.
[41] Acrónimo acuñado durante la Segunda Guerra Mundial, derivado de la expresión inglesa radio detecting and ranging: detección y medición de distancias mediante ondas de radio.
[42] Algunos del Instituto de Estudios Avanzados de Princeton (Institute for Advanced Study), donde estaban, o por donde pasaron, Albert Einstein, Kurt Gödel, J. Robert Oppenheimer, John von Neumann, Benoit Mandelbrot, T. S. Eliot, Thomas Mann, Hannah Arendt o Herman Broch, y cuyo fundador y primer director, Abraham Flexner, dijo: «No ignoro que he esbozado una utopía educativa. He amarrado deliberadamente el Instituto a una estrella; sería un error comenzar con cualquier otra ambición o aspiración.» Otros eran W. R. Ashby, A. Newell, W. S. McCulloch, H. A. Simon o E. F. Moore.
[43] Husbands, P. and Holland, O. (2008), The Ratio Club: A Hub of British Cybernetics. En: Husbands, P., Holland, O., and Wheeler, M., editors, The Mechanical Mind in History, pages 91–148. The MIT Press.
[44] Wiener, N. (1988), Cibernética, Tusquets.
[45] Shannon, C. E. (1948). A Mathematical Theory of Communication. The Bell System Technical Journal, XXVII(3):379–423.
[46] Otros requisitos eran ‘ser listo como el demonio’ y ‘no ser Catedrático’.
[47] En la propuesta de Dartmouth Marvin Minsky dice: «El resultado importante que se buscaría sería que la máquina tendería a construir modelos abstractos internos del entorno en el que se encuentra». Igualmente había utilizado la expresión ‘goal–seeking’, que sería la utilizada por W. Ross Ashby en su trabajo sobre el homeostato, del que hablaremos más adelante (McCarthy et al., op. cit., p. 6). Una idea similar se puede encontrar en el libro de David Eagleman, El cerebro (libro y serie de TV).
[48] En su libro hacía esta advertencia sobre los peligros del reduccionismo: «En lugar de que su teoría sea tan amplia como la realidad, su percepción de la realidad puede ser tan estrecha como su teoría.»
[49] Desde el 14 de septiembre de 1949 hasta el 15 de septiembre de 1955, aunque hubo una última reunión, la número 38, el 27 de noviembre de 1958 en la que se celebró el simposio “Mecanización del Proceso de Pensamiento”.
[50] Ashby, W. R. (1949). The Electronic Brain. Radio Electronics, March:77–80. p. 77.
[51] Dewhurst, J. (Online: 28 Aug 2018). British cybernetics. En: Sprevak, M. and Colombo, M., editors, The Routledge Handbook of the Computational Mind, pages 29–69. Routledge.
[52] Ashby, W. R. (1954). Design for a Brain. John Wiley & Sons. cap. 7.
[53] Ashby, op. cit., cap. 9.
[54] Walter, W. G. (1981). El cerebro viviente. Fondo de Cultura Económica.
[55] Walter, op. cit., p. 119.
[56] Ver una descripción detallada en el capítulo V de la obra citada. Una grabación en video de las dos tortugas ‘especulando’ en el salón de los Walter en Bristol se puede ver en: https://www.youtube.com/watch?v=lLULRlmXkKo.
[57] Walter, W. G. (1950). An Imitation of Life. Scientific American, 182:42–45. p. 44.
[58] Una versión en español, “Un cálculo lógico de las ideas inmanentes en la actividad nerviosa”, se puede encontrar en el capítulo I del libro de Margaret Boden, Filosofía de la Inteligencia Artificial (Fondo de Cultura Económica, 1994).
[59] M. Boden, op. cit., p. 34.
[60] Arbib, M. A. (1982). Cerebros, máquinas y matemáticas. Alianza.
[61] M. Boden, op. cit., p. 35.
[62] Ver [https://en.wikipedia.org/wiki/Homeostat].
[63] Turing, A. M. (1937). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, s2-42(1):230–265.
[64]Turing, A. M. (1950). Computing Machinery and Intelligence. Mind, LIX (236): 433–460.
[65] Ver el post Turing y Wittgenstein en Cambridge, publicado por Adyacente Posible el 22/06/2025.
[66] Turing, op. cit. p. 435.
[67] Turing, op. cit., p. 442.
[68] Turing, op. cit., p. 433.
[69] Gómez-Tejedor, S. B. and Peirano, M. (2009). El rival de Prometeo. Impedimenta.
[70] «Un carácter algo extraño. Gordo, irascible, torpe:/un solterón cascarrabias quejoso de mal de orejas», según Hans Magnus Enzensberger en Los elixires de la ciencia.
[71] Poe, E. A. (1973). Ensayos y críticas. Alianza, p.186–213.
[72] Wheeler, M. (2008). God’s Machines: Descartes on the Mechanization of Mind. En: Husbands, P., Holland, O., and Wheeler, M., editors, The Mechanical Mind in History, pages 307–330. MIT Press.
[73] Schwartz, O. (2019). Untold History of AI: Charles Babbage and the Turk. IEEE Spectrum, March; Essinger, J. (2015). El algoritmo de Ada. Alba.
[74] Turing, op. cit., p. 450.
[75] Schwartz, op. cit.; Essinger, op. cit.
[76] Turing, op. cit., p. 450. La inspiración es sobre todo transpiración.
[77] Turing, op. cit., p. 454.
[78] Walter introducía una idea similar cuando especulaba: «no hay necesidad lógica o experimental de invocar algo más que el número para dar cuenta de nuestra convicción subjetiva de libre albedrío y nuestra conciencia objetiva de personalidad en nuestros semejantes» (Walter, 1950, p. 44).
[79] Turing, op. cit., p. 454.
[80] Harry Harrison y Marvin Minsky imaginaron una realización de las ideas de Turing en su novela The Turing Option (Viking 1992); Ian McEwan propone una historia alternativa en la que Turing no se suicida en Máquinas como yo (Anagrama 2019).
[81]Leavitt, D. (2007). El hombre que sabía demasiado. Alan Turing y la invención de la computadora. Antoni Bosch.
[82] Nilsson, N. J. (2010). The Quest for Artificial Intelligence. A History of Ideas and Achievements. http://www.cambridge.org/us/0521122937.
[83] Kneale, W. and Kneale, M. (1980). El desarrollo de la lógica. Tecnos, p. 64.
[84] «Dos son, en efecto, los requisitos de la demostración: premisas, o puntos de partida, verdaderas y argumentaciones válidas» (Kneale and Kneale, op. cit., p. 1).
[85] Superada en su aspecto apodíctico, la lógica aristotélica vuelve a tomar auge en el dialéctico.
[86] B, 2 996b26-30.
[87] Aristóteles, “Sobre la interpretación”, cap. 9, en Organon II. Vemos que en el propio Aristóteles está el origen de las lógicas polivalentes e infinitamente valuadas, como la lógica borrosa. Habría que destacar que el énfasis en la naturaleza contingente de las cosas reales por venir, y en ellas se cifra el futuro, niega la necesidad y el determinismo.
[88] Jan Łukasiewicz (1975), Observaciones filosóficas sobre los sistemas polivalentes de la lógica proposicional, Estudios de lógica y filosofía, Revista de Occidente.
[89] Kneale and Kneale, op. cit., p. 530 y ss.
[90] De ahí su nombre fuzzy: borroso, difuso.
[91] Ver Kneale and Kneale, op. cit., p. 374ss y el capítulo siguiente.
[92] Zadeh, L. A. (1965). Fuzzy Sets. Information and Control, 8:338–353.
Vinagre, Blas M. «En torno a Turing». Adyacente posible, 12 de febrero de 2026. https://adyacenteposible.com/2026/02/12/en-torno-a-turing-el-hombre-entre-las-maquinas-blas-vinagre/
